если последнее стремится к нулю при σ→∞, то (3.38) будет пределом выражения (3.37). Другими словами, распределения функций f(t, γ) и f(t+σ, γ) становятся асимптотически независимыми, когда σ→∞. Более общим, но совершенно аналогичным рассуждением можно показать, что одновременное распределение функций f(t1, γ), …, f(tn, γ) и функций f(σ+s1, γ), …, f(σ+sm, γ) стремится к совместному распределению первого и второго множества, когда σ→∞. Другими словами, если F[f (t, γ)] - любой ограниченный измеримый функционал, т. е. величина, зависящая от всего распределения значений функции f(t, γ) от t, то для него должно выполняться условие
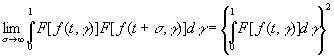. (3.40)
Если F[f (t, γ)] инвариантен при сдвиге по t и принимает только значения 0 или 1, то
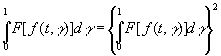, (3.41)
т. е. группа преобразований f(t, γ) в f(t+σ, γ) метрически транзитивна. Отсюда следует, что если F[f (t, γ)] - любой интегрируемый функционал от f как функции от t, то по эргодической теореме
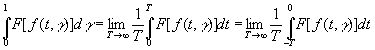(3.42)
[c.138]
для всех значений γ, исключая множество нулевой меры. Таким образом, мы почти всегда можем определить любой статистический параметр такого временного ряда (и даже любого счетного множества статистических параметров) из прошлой истории одного только параметра. В самом деле, если для такого временного ряда мы знаем
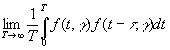(3.43)
то мы знаем Ф(t) почти во всех случаях и располагаем полным статистическим знанием о временном ряде.
Некоторые величины, зависящие от временного ряда такого рода, обладают интересными свойствами. В частности, интересно знать среднее значение величины
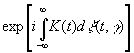(3.44)
Формально мы можем записать его в виде
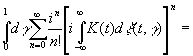
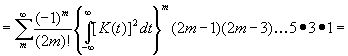
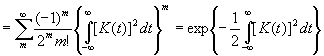. (3.45)
Весьма интересная задача - попытаться построить возможно более общий временной ряд из простых рядов броунова движения. При таких построениях, как подсказывает пример рядов Фурье, разложения типа (3.44) составляют удобные строительные блоки. В частности, исследуем временные ряды специального вида:
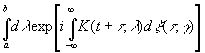(3.46)
[c.139]
Предположим, что нам известна функция ξ(τ, γ), а также выражение (3.46). Тогда при t1>t2 находим, как в (3.45),
(3.47)
Умножив на
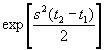
и положив s(t2-t1)=iσ, получим при t2→t1
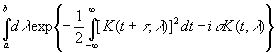(3.48)
Примем K(t1, λ) за новую независимую переменную μ и, решая относительно λ, получим
(3.49)
Тогда выражение (3.48) будет иметь вид
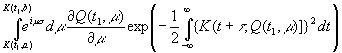(3.50)
Отсюда преобразованием Фурье можно найти
(3.51)
как функцию от μ, коль скоро μ лежит между K(t1, a) и K(t1, b). Интегрируя эту функцию по μ, найдем
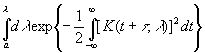(3.52)
[c.140]
как функцию от K(t1, λ) и t1. Иначе говоря, существует известная функция F (u, v), такая, что
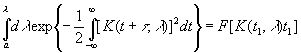(3.53)
Поскольку левая часть этого равенства не зависит от t1, мы можем обозначить ее через G(λ) и положить
(3.54)
Здесь F - известная функция, и ее можно обратить относительно первого аргумента, положив
, (3.55)
где H - также известная функция. Отсюда
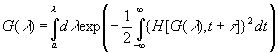(3.56)
Тогда выражение
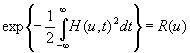(3.57)
будет известной функцией и
(3.58)
откуда
, (3.59)
или
. (3.60)
Входящую в это выражение константу можно определить из соотношения
, (3.61)
или
. (3.62)
Очевидно, что если а конечно, то безразлично, какое значение мы ему дадим; в самом деле, наш оператор не [c.141] изменится от прибавления одной и той же величины ко всем значениям λ. Поэтому можно взять а=0. Таким образом, мы определили λ как функцию от G и, следовательно, G - как функцию от λ. Из (3.55) следует, что мы тем самым определили K(t, λ). Для завершения расчетов нам нужно только найти b. Это число можно определить сравнением выражений
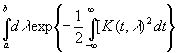(3.63)
и
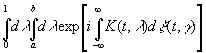. (3.64)
Таким образом, если при некоторых условиях, которые еще остается точно сформулировать, временной ряд допускает запись в виде (3.46) и известна функция ξ(t, γ) то мы можем определить функцию K(t, λ) в (3.46) и числа а и b с точностью до неопределенной константы, прибавляемой к а, λ и b. Не возникает особых трудностей при b→+∞, также не слишком сложно распространить эти рассуждения на случай а→ -∞. Конечно, предстоит проделать еще немалую работу, рассматривая задачу обращения функций в случае, когда результаты не однозначны, и общие условия справедливости соответствующих разложений. Тем не менее мы по крайней мере сделали первый шаг к решению задачи приведения обширного класса временных рядов к каноническому виду, что чрезвычайно важно для конкретного формального применения теорий предсказания и измерения информации, намеченных выше в этой главе.