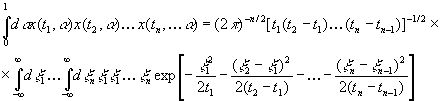(3.19)
при условии 0 ≤t1 ≤…≤ tn. Положим
(3.20)
[c.132]
где λk,1+λk,2+…+λk,n=n.Тогда выражение (3.19) примет значение
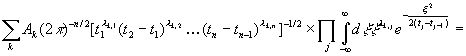
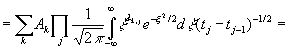
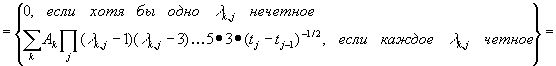
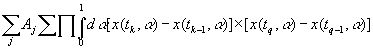. (3.21)
Здесь первая сумма берется по j; вторая - по всем способам разбиения n элементов на пары в группах, включающих соответственно λk,1, …, λk,n элементов; произведение - по парам значений k и q, где λk,1 элементов среди выбранных tk и tq равны t1, λk,2 элементов равны t2 и т. д. Отсюда сразу же следует
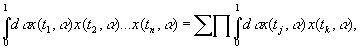(3.22)
[c.133]
где сумма берется по всем разбиениям величин t1, …, tnна различные пары, произведение - по всем парам в каждом разбиении. Другими словами, если нам известны средние значения попарных произведений величин x(tj, α), то нам известны и средние значения всех многочленов от этих величин и, следовательно, их полное статистическое распределение.
До сих пор мы рассматривали броуновы перемещения x (tj,α), в которых t положительно. Положив
, (3.23)
где α и β имеют независимые равномерные распределения в интервале (0, 1), получим распределение для ξ(t, α, β), где t пробегает всю бесконечную действительную ось. Существует хорошо известный математический прием отобразить квадрат на прямолинейный отрезок таким образом, что площадь преобразуется в длину. Надо лишь записать координаты квадрата в десятичной форме
(3.24)
и положить
,
и мы получим искомое отображение, являющееся взаимно однозначным почти для всех точек как прямолинейного отрезка, так и квадрата. Используя эту подстановку, введем
. (3.25)
Теперь мы хотим определить в некотором подходящем смысле
(3.26)
Сразу приходит мысль определить указанное выражение как интеграл Стильтьеса, но это встречает [c.134] препятствие в том, что ξ представляет собой весьма нерегулярную функцию от t. Однако если К приближается достаточно быстро к нулю при t→± ∞ и является достаточно гладкой функцией, то разумно положить
(3.27)
При этих условиях мы формально получим
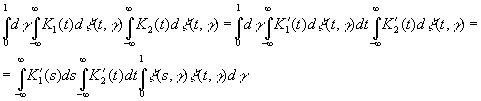(3.28)
Если теперь t и s имеют противоположные знаки, то
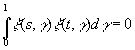(3.29)
а если они одного знака и |s|<|t|, то
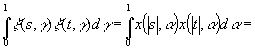
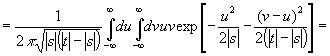
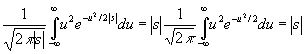(3.30)
[c.135]
Отсюда
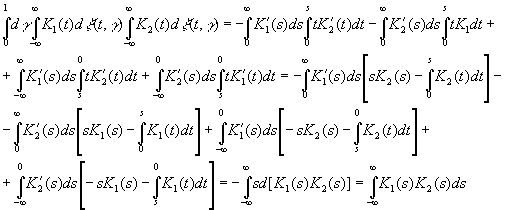
(3.31)
В частности,
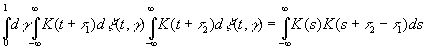(3.32)
Более того,
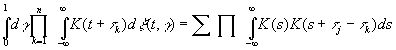(3.33)
[c.136]
где сумма берется по всем разбиениям величин τ1, …, τn на пары, а произведение - по парам в каждом разбиении. Выражение
(3.34)
изображает очень важный ансамбль временных рядов по переменной t, зависящих от некоторого параметра распределения γ. Доказанное нами равносильно утверждению, что все моменты и, следовательно, все статистические параметры этого распределения зависят от функции
(3.35)
представляющей собой известную в статистике автокорреляционную функцию со сдвигом τ. Таким образом, распределение функции f(t, γ) имеет те же статистики, что и функция f(t+t1, γ); и действительно, можно доказать, что если
, (3.36)
то преобразование параметра γ в Г сохраняет меру. Другими словами, наш временной ряд f(t, γ) находится в статистическом равновесии.
Далее, если мы рассмотрим среднее значение для
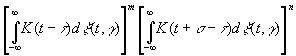(3.37)
то оно состоит в точности из членов выражения
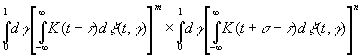(3.38)
[c.137]
и из конечного числа членов, имеющих множителями степени выражения
, (3.39)