Первая разновидность - так называемые линейные инварианты. Обозначим через х элементы, преобразуемые абелевой группой, и пусть f(x) - комплексная функция этих элементов, обладающая надлежащими свойствами непрерывности или интегрируемости. Тогда, если Тх - элемент, получаемый из х при преобразовании Т, a f(x) - функция с абсолютным значением 1, такая, что
f (Tx) = α(T) f(x), (2.03)
где α(T) - число с абсолютным значением 1, зависящее только от Т, то f(x) мы будем называть характером группы.
Это инвариант группы в несколько обобщенном смысле. Ясно, что если f(x) и g(x) - характеры группы, то f(x)g(x) также есть характер группы, как и [f(x)] . Если какая-либо функция h(x), определенная на группе, представима линейной комбинацией характеров группы, скажем в виде
, (2.04)
где fk(x) - характер группы, и если αk(T) находится в таком же отношении к fk(x), как α(T) - к f(x) в (2.03), то [c.108]
(2.05)
Таким образом, коль скоро h(x) допускает разложение по некоторому множеству характеров группы, то и h(Tx) при всех Т допускает такое разложение.
Мы видели, что характеры группы порождают другие характеры при умножении и обращении; нетрудно видеть также, что константа 1 есть характер. Следовательно, умножение на характер порождает группу преобразований самих характеров; последняя называется группой характеров исходной группы.
Если исходная группа есть группа сдвигов по бесконечной прямой, то оператор Т изменяет х в х+Т и соотношение (2.03) переходит в соотношение
, (2.06)
которое выполняется при f(x)=e, α(T)= e. Характерами будут функции e, а группой характеров будет группа сдвигов, изменяющая λ в λ+τ и, следовательно, имеющая такое же строение, как и исходная группа. Но дело будет обстоять иначе, если исходная группа состоит из поворотов по окружности. В этом случае оператор Т изменяет х в число, лежащее между 0 и 2π и отличающееся от х+Т на целочисленное кратное 2π. Соотношение (2.06) еще справедливо, но у нас появляется добавочное условие
. (2.07)
Положив вновь f(x) = e, получим
. (2.08)
Это значит, что λ должно быть целым действительным числом - положительным, отрицательным или нулем. Следовательно, группа характеров здесь соответствует сдвигам целых действительных чисел. С другой стороны, если исходная группа есть группа сдвигов целых чисел, то х и Т в (2.06) могут принимать только целочисленные значения и функция e задается полностью числом, лежащим между 0 и 2π и отличающимся от λ на целочисленное кратное 2π. Следовательно, группа характеров в этом случае по существу представляет собой группу поворотов по окружности.
В любой группе характеров числа α(T), соответствующие данному характеру f, распределены таким образом, [c.109] что это распределение не нарушается при умножении их всех на α(S), каков бы ни был элемент S исходной группы. Иначе говоря, если есть какое-то разумное основание взять среднее от этих чисел, не затрагиваемое, когда группа преобразуется умножением каждого ее преобразования на одно фиксированное, то либо α(Т) тождественно равно 1, либо наше среднее инвариантно относительно умножения на числа, отличные от 1, и потому должно равняться 0. Отсюда можно заключить, что среднее произведение характера на величину, с ним сопряженную (которая также является характером), будет равно 1, а среднее произведение характера на величину, сопряженную с другим характером, будет равно 0. Другими словами, если h(x) представлено как в (2.04), то
(2.09)
Для группы поворотов по окружности это дает нам сразу, что если
(2.10)
то
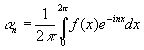(2.11)
Для сдвигов же по бесконечной прямой результат тесно связан с тем обстоятельством, что если в некотором подходящем смысле
(2.12)
то в определенном смысле
(2.13)
Эти результаты изложены здесь очень грубо, без точной формулировки условий их справедливости. Более строгое изложение теории читатель может найти в работе, указанной в примечании. [c.110]
Наряду с теорией линейных инвариантов группы, существует также общая теория ее метрических инвариантов. Последние представляют собой системы меры Лебега, не претерпевающие изменений, когда объекты, преобразуемые группой, переставляются операторами группы. В этой связи следует упомянуть интересную теорию групповой меры, которую дал Гаар. Как мы видели, всякая группа сама есть собрание объектов, которые переставляются между собой при умножении на операторы данной группы. Поэтому она может иметь инвариантную меру. Гаар доказал, что некоторый довольно широкий класс групп имеет однозначно определенную инвариантную меру, задаваемую строением самой группы.
Наиболее важное применение теории метрических инвариантов группы преобразований состоит в обосновании взаимной заменимости фазовых и временных средних, которую, как мы видели выше, Гиббс тщетно пытался доказать. Это доказательство было выполнено на основе так называемой эргодической теории.
В обычных эргодических теоремах рассматривается ансамбль Е, меру которого можно принять за единицу, и этот ансамбль преобразуется в себя сохраняющим меру преобразованием Т или группой сохраняющих меру преобразований Т, где -∞<λ<∞ и
(2.14)
Эргодическая теория имеет дело с комплексным функциями f(х) элементов х из Е. Во всех случаях f(х) считается измеримой по х, а если мы рассматриваем непрерывную группу преобразований, то f(Тх) считается измеримой по х и λ вместе.
В эргодической теореме Купмена - фон Неймана о сходимости в среднем функция f(х) считается принадлежащей к классу L; это значит, что
(2.15)
Теорема утверждает, что [c.111]
(2.16)
или соответственно
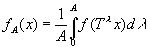(2.17)
сходится в среднем к пределу f(х) при N→∞ или соответственно при А→∞ в том смысле, что
(2.18)