Коллектив авторов - Логика: Шпаргалка стр 10.

Истинность одного из противоположных суждений определяет ложность другого: А → ⌉Е; Е → ⌉A. Напр., истинность суждения "Все офицеры – военнослужащие" определяет ложность суждения "Ни один офицер не является военнослужащим". При ложности же одного из противоположных суждений другое остается неопределенным – оно может быть как истинным, так и ложным: ⌉A → (Е ∨ ⌉Е); ⌉Е → (А ∨ ⌉A).

2. Противоречащими (контрадикторными) являются суждения А и О, Е и I, которые одновременно не могут быть ни истинными, ни ложными.

Для противоречия характерна строгая, или альтернативная, несовместимость: при истинности одного из суждений другое всегда будет ложным; при ложности первого второе будет истинным. Отношения между такими суждениями регулируются законом исключенного третьего.

Если А признается истинным, то О будет ложным (А → ⌉О); при истинности Е будет ложным I: (Е → ⌉I). И наоборот: при ложности А будет истинным О (⌉A → О); а при ложности Е будет истинным I (⌉Е → I).

29. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ СУЖДЕНИЯМИ

Отношения устанавливаются не между любыми, а лишь между сравнимыми, т. е. имеющими общий смысл суждениями.

Несравнимыми являются суждения, имеющие различные субъекты или предикаты. Таковы, напр., два суждения: "Среди космонавтов есть летчики"; "Среди космонавтов есть женщины".

Сравнимыми являются суждения с одинаковыми субъектами и предикатами и различающиеся связкой или квантором. Напр.: "Все американские индейцы живут в резервациях"; "Некоторые американские индейцы не живут в резервациях".

Отношения между простыми суждениями обычно рассматриваются с помощью мнемонической схемы, называемой логическим квадратом. Его вершины символизируют простые категорические суждения – А, Е, I, О; стороны и диагонали – отношения между суждениями.

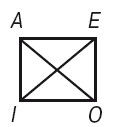
Среди сравнимых различают совместимые и несовместимые суждения.

Совместимыми являются суждения, которые одновременно могут быть истинными. Различают три вида совместимости: эквивалентность (полная совместимость), частичная совместимость (субконтрарность) и подчинение.

1. Эквивалентными являются такие суждения, которые имеют одинаковые логические характеристики: одинаковые субъекты и предикаты, однотипную – утвердительную или отрицательную – связку, одну и ту же выраженную квантором количественную характеристику.

С помощью логического квадрата отношения между простыми эквивалентными суждениями не иллюстрируются.

2. Частичная совместимость характерна для суждений I и О, которые могут быть одновременно истинными, но не могут быть одновременно ложными. При ложности одного из них другое будет истинным: ⌉1→0,⌉0 → I. Напр., при ложности суждения "Некоторые злаки ядовиты" будет истинным суждение "Некоторые злаки не являются ядовитыми". В то же время при истинности одного из частных суждений другое может быть как истинным, так я ложным: I → (О ∨ ⌉0); O → (I ∨ ⌉I).

3. Подчинение имеет место между суждениями А и I, Е и О. Для них характерны следующие две зависимости.

При истинности общего суждения частное всегда будет истинным: А → I, Е → О. Напр., при истинности общего суждения "Всякое правоотношение регулируется нормами права" истинным будет и частное – "Некоторые правоотношения регулируются нормами права". При истинности суждения "Ни один кооператив не относится к государственным организациям" будет истинным и суждение "Некоторые кооперативы не относятся к государственным организациям".

При ложности частного суждения общее суждение также будет ложным: ⌉I → ⌉A; ⌉O → ⌉E.

При подчинении остаются неопределенными следующие зависимости: при ложности общего суждения подчиненное частное может быть как истинным, так и ложным: ⌉А → (I ∨⌉I); ⌉Е → (О ∨ ⌉О); при истинности подчиненного частного общее может быть как истинным, так и ложным: I → (А ∨ ⌉А); О → (Е ∨⌉Е).

30. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ СЛОЖНЫМИ СУЖДЕНИЯМИ

Сложные суждения могут быть сравнимыми и несравнимыми.

Несравнимые – это суждения, которые не имеют общих пропорциональных переменных. Напр.,

р ∧qи m∧ n.

Сравнимые – это суждения, которые имеют одинаковые пропозиционные переменные (составляющие) и различаются логическими связками, включая отрицание. Напр., сравнимыми являются следующие два суждения: "Норвегия или Швеция имеют выход в Балтийское море" (р ∨ q); "Ни Норвегия, ни Швеция не имеют выхода в Балтийское море" (⌉ р ∧ ⌉q).

Сложные сравнимые суждения могут быть совместимыми и несовместимыми.

Совместимыми являются такие сравнимые суждения, которые одновременно могут быть истинными. Различают три вида совместимости сложных суждений: эквивалентность, частичная совместимость и подчинение.

1. Эквивалентные – это суждения, которые принимают одни и те значения, т. е. одновременно являются либо истинными, либо ложными.

Отношение эквивалентности позволяет выражать одни сложные суждения через другие – конъюнкцию через дизъюнкцию или импликацию, и наоборот.

1. Выражение конъюнкции через дизъюнкцию: ⌉(А ∧ 6) ≡ ⌉А ∨ ⌉В.

2. Выражение дизъюнкции через конъюнкцию: ⌉(А ∨ В) ≡ ⌉А ∧ ⌉В.

3. Выражение импликации через конъюнкцию: А → В ≡ (А ∧ ⌉В)].

4. Выражение импликации через дизъюнкцию: А → В ≡ ⌉А ∨ В].

2. Частичная совместимость характерна для суждений, которые могут быть одновременно истинными, но не могут быть одновременно ложными.

3. Подчинение между суждениями имеет место в том случае, когда при истинности подчиняющего подчиненное всегда будет истинным.

31. МОДАЛЬНОСТЬ СУЖДЕНИЙ. ЭПИСТЕМИЧЕСКАЯ МОДАЛЬНОСТЬ

Суждение как форма мышления содержит двоякого рода информацию – основную и дополнительную. Основная информация находит явное выражение в субъекте и предикате суждения, в логической связке и кванторах. Дополнительная информация относится к характеристике логического или фактического статуса суждения, к оценочным и другим его характеристикам. Такая информация называется модальностью суждения. Она может быть выражена отдельными словами, а может и не иметь явного выражения. В этом случае ее выявляют анализом контекста.

Модальность – это явно или неявно выраженная в суждении дополнительная информация о степени его обоснованности, логическом или фактическом статусе, о регулятивных, оценочных и других его характеристиках.

Эпистемическая (от греч. эпистема – высший тип достоверного знания) модальность – это выраженная в суждении информация об основаниях его принятия и степени обоснованности. К таким основаниям относится вера и знание.

По эпистемическому статусу вера – это стихийное, некритическое принятие чужих мнений, истинных или ложных, прогрессивных или реакционных

Знание как логическое обоснование – это принятие суждения как истинного или ложного в силу его обоснованности другими суждениями, из которых принимаемое суждение логически вытекает как следствие.

По степени обоснованности среди знаний различают два непересекающихся класса суждений: достоверные и проблематичные.

1. Достоверные суждения – это достаточно обоснованные истинные или ложные суждения.

Их истинность или ложность устанавливается либо путем непосредственной проверки, либо опосредованно, когда суждение подтверждается эмпирическими или теоретическими положениями.

Достоверность относится к такой модальной характеристике суждения, которая, подобно понятиям истины и лжи, не изменяется по степеням. О двух высказываниях нельзя сказать, что одно из них "более достоверно", чем другое. В случае достаточной обоснованности суждения его считают доказанным, тем самым достоверным, т. е. истинным или ложным без изменения по степеням.

2. Проблематичные суждения – это суждения, которые нельзя считать достоверными в силу их недостаточной обоснованности. Поскольку истинность или ложность таких суждений точно не установлена, то они лишь претендуют быть таковыми. Отсюда и названия их: проблематичные, правдоподобные или вероятные.

В естественном языке показателями проблематичности суждения обычно служат вводные слова: по-видимому, вероятно, представляется, возможно, можно предположить и др.

В судебном исследовании в форме проблематичных суждений строятся версии (гипотезы) об обстоятельствах расследуемых дел. Будучи обоснованными, правдоподобные суждения направляют расследование по правильному руслу и способствуют установлению по каждому делу достоверных результатов.

Обоснованность проблематичных суждений может быть представлена в терминах теории вероятности.