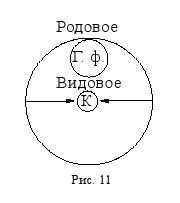
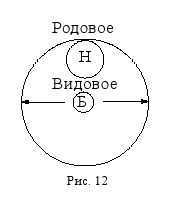
Обобщение понятия – это логическая операция перехода от видового понятия к родовому с помощью исключения из его содержания какого-либо признака (или нескольких признаков). Содержание понятия, лишённое каких-то признаков, уменьшается, но при этом автоматически увеличивается объём понятия, которое из видового становится родовым или обобщается. Например, если от содержания понятия "биология" (Б) отбросить признак "изучать различные формы жизни", то оно превратится в понятие "наука" (Н), которое будет родовым по отношению к исходному видовому понятию "биология" (рис. 12).
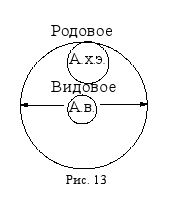
Так же, если от содержания понятия "атом водорода" (А. в.) отбросить признак "иметь один электрон", то оно превратится в понятие "атом химического элемента" (А. х. э.), которое будет родовым по отношению к исходному видовому понятию "атом водорода" (рис. 13).
Ограничения и обобщения понятий складываются в логические цепочки, в которых каждое понятие (за исключением начального и конечного) является видовым по отношению к одному соседнему понятию и родовым по отношению к другому. Например, если последовательно обобщать понятие "Солнце", то получится следующая цепочка: Солнце → звезда → небесное тело→ → физическое тело → форма материи. В этой цепочке понятие "звезда" является родовым по отношению к понятию "Солнце", но видовым по отношению к понятию "небесное тело"; так же понятие "небесное тело" является родовым по отношению к понятию "звезда", но видовым по отношению к понятию "физическое тело" и т. д. Движение по нашей цепочке от понятия "Солнце" к понятию "форма материи" представляет собой серию последовательных обобщений, а движение в обратном направлении – серию ограничений. Если изобразить отношения между понятиями из указанной цепочки на схеме Эйлера, то получатся круги, последовательно располагающиеся один в другом: самый маленький будет обозначать понятие "Солнце", а самый большой – "форма материи".
Пределом цепочки ограничения любого понятия всегда будет какое-либо единичное понятие (см. раздел 1.1.), а пределом цепочки обобщения, как правило, будет какое-либо широкое, философское понятие, например: объект мироздания, форма материи или форма бытия.
Наиболее частые ошибки, которые допускают при ограничении и обобщении понятий, заключаются в том, что вместо вида для какого-то рода называют часть из некого целого, и вместо рода для какого-то вида называют целое по отношению к какой-либо части. Например, в качестве ограничения понятия "цветок" предлагают понятие "стебель". Действительно, стебель – это часть цветка, но ограничить понятие – значит подобрать не часть для целого, а вид для рода. Следовательно, правильным ограничением понятия "цветок" будет понятие "ромашка", или "тюльпан", или "хризантема" и т. п. В качестве обобщения понятия "дерево" нередко предлагают понятие "лес". Конечно же, лес является неким целым по отношению к деревьям, из которых он состоит, но обобщить понятие – значит подобрать не целое для части, а род для вида. Следовательно, правильным обобщением понятия "дерево" будет понятие "растение", или "объект флоры", или "живой организм" и т. п.
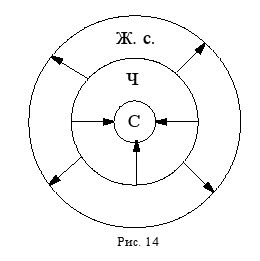
Итак, почти любое понятие (за исключением единичных и широких, философских) можно как ограничить, так и обобщить. Другими словами, подобрать для него как видовое понятие, так и родовое. Например, ограничением понятия "человек" (Ч) будет понятие "спортсмен" (С) или "писатель", или "мужчина", или "молодой человек" и т. п., а его обобщением будет понятие "живое существо" (Ж. с.) (рис. 14).
Проверьте себя:
1. Что такое ограничение понятия?
2. Что представляет собой логическая операция обобщения понятия?
3. Каким образом ограничения и обобщения понятий складываются в логические цепочки? Каковы пределы цепочек ограничений и обобщений?
4. Какие ошибки часто допускают при ограничении и обобщении понятий? Продемонстрируйте на самостоятельно подобранных примерах, что целое и часть нельзя путать с видом и родом.
5. Всякое ли понятие можно подвергнуть ограничению или обобщению? Какие понятия не поддаются этим логическим операциям?
6. Подберите десять любых понятий и проделайте с ними ограничение и обобщение, т. е. подберите для каждого как видовое, так и родовое понятие, иллюстрируя эти операции схемами Эйлера.
1.5. Операция определения понятия
Определение понятия – это логическая операция, которая раскрывает содержание понятия.
Определения бывают явными и неявными.
Явное определение непосредственно раскрывает содержание понятия, даёт прямой ответ на вопрос, чем является объект, который оно обозначает. Например: "Термометр – это физический прибор, предназначенный для измерения температуры", – явное определение.
Неявное(контекстуальное) определение раскрывает содержание понятия не прямо, а косвенно, с помощью контекста, в котором это понятие употребляется. Например, из следующей фразы: "Во время этого грандиозного эксперимента сверхточные термометры зафиксировали температуру в 1 000 °C", – косвенно следует ответ на вопрос: "Что такое термометр?" – вытекает неявное определение этого понятия. Понятно, что определениями в полном смысле этого слова надо считать явные определения. В дальнейшем речь пойдёт именно о них.
Определения также бывают реальными и номинальными.
Реальное определение раскрывает содержание понятия, обозначающего какой-то объект, т. е. они посвящены объектам. Например:
"Термометр – это физический прибор, предназначенный для измерения температуры" – реальное определение.
Номинальное (от лат. nomen – имя) раскрывает значение термина, которым выражено какое-либо понятие, т. е они посвящены терминам (словам). Например: "Слово "термометр" обозначает физический прибор, предназначенный для измерения температуры", – номинальное определение.
Как видим, принципиальной разницы между реальными и номинальными определениями не существует. Они различаются, как правило, по форме, но не по сути.
Существует несколько способов определения понятия, но среди них выделяется классический способ, который заключается в том, что определяемое понятие подводится под ближайшее к нему родовое понятие, после чего следует указание на его видовое отличие. Например, определение: "Астрономия – это наука о небесных телах", – построено по классическому способу. В нём определяемое понятие "астрономия" сначала подводится под ближайшее к нему родовое понятие "наука" (астрономия – это обязательно наука, но наука – это не обязательно астрономия), а потом указывается на видовое отличие астрономии от других наук: "…о небесных телах". Пользуясь классическим способом, вы сможете дать точное и правильное определение любому понятию, конечно, если определяемый объект или термин вам хорошо знаком, и вы знаете, что он собой представляет или что означает, соответственно. Например, нам требуется дать определение понятию "квадрат". Следуя классическому способу, сначала подведём его под родовое понятие: "Квадрат – это геометрическая фигура", – а затем укажем его видовое отличие от других геометрических фигур, которое заключается в наличии равных сторон и прямых углов. Итак: "Квадрат – это геометрическая фигура, у которой все стороны равны и углы прямые". Давая определение понятию "квадрат", мы могли бы подвести его под более близкое родовое понятие "прямоугольник", и тогда определение получилось бы следующим: "Квадрат – это прямоугольник, у которого все стороны равны", – однако и приведённое выше определение квадрата раскрывает содержание соответствующего понятия и является верным. Обратите внимание на то, что фактически все определения, встречающиеся в научной, учебной и справочной литературе, например в толковых словарях, построены по классическому способу.
Существует несколько логических правил определения. Нарушение хотя бы одного из них приводит к тому, что содержание понятия не раскрывается и определение не достигает своей цели, являясь неверным. Рассмотрим эти правила и ошибки, возникающие при их нарушении: