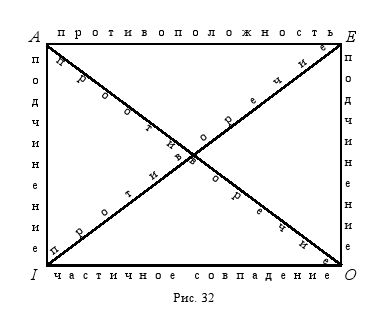
Вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так, суждения вида A и вида I, а также суждения вида E и вида O находятся в отношении подчинения. Суждения вида A и вида E находятся в отношении противоположности, а суждения вида I и вида O – частичного совпадения. Суждения вида A и вида O, а также суждения вида E и вида I находятся в отношении противоречия. Неудивительно, что логический квадрат не изображает отношение равнозначности, потому что в этом отношении находятся одинаковые по виду суждения, т. е. равнозначность – это отношение между суждениями A и A, I и I, E и E, O и O. Чтобы установить отношение между двумя суждениями, достаточно определить, к какому виду относится каждое из них. Например, надо выяснить, в каком отношении находятся суждения: "Все люди изучали логику", "Некоторые люди не изучали логику". Видя, что первое суждение является общеутвердительным (A), а второе частноотрицательным (O), мы без труда устанавливаем отношение между ними с помощью логического квадрата – противоречие. Суждения: "Все люди изучали логику (A)", "Некоторые люди изучали логику (I)", находятся в отношении подчинения, а суждения: "Все люди изучали логику (A)", "Все люди не изучали логику (E)", – находятся в отношении противоположности.
Как уже говорилось, важным свойством суждений, в отличие от понятий, является то, что они могут быть истинными или ложными.
Что касается сравнимых суждений, то истинностные значения каждого из них определённым образом связаны с истинностными значениями остальных. Так, если суждение вида A является истинным или ложным, то три других (I, E, O), сравнимых с ним суждения (имеющих сходные с ним субъекты и предикаты), в зависимости от этого (от истинности или ложности суждения вида A) тоже являются истинными или ложными. Например, если суждение вида A: "Все тигры – это хищники", – является истинным, то суждение вида I: "Некоторые тигры – это хищники", – также является истинным (если все тигры – хищники, то и часть из них, т. е. некоторые тигры – это тоже хищники), суждение вида E: "Все тигры – это не хищники", – является ложным, и суждение вида O: "Некоторые тигры – это не хищники", – также является ложным. Таким образом, в данном случае из истинности суждения вида A вытекает истинность суждения вида I и ложность суждений вида E и вида O (разумеется, речь идёт о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).
Проверьте себя:
1. Какие суждения называются сравнимыми и какие – несравнимыми?
2. Что такое совместимые и несовместимые суждения? Приведите по три примера совместимых и несовместимых суждений.
3. В каких отношениях могут быть совместимые суждения? Приведите по два примера для отношений равнозначности, подчинения и частичного совпадения.
4. В каких отношениях могут быть несовместимые суждения?
Приведите по три примера для отношений противоположности и противоречия. Почему противоположные суждения могут быть одновременно ложными, а противоречащие не могут?
5. Что представляет собой логический квадрат? Каким образом он изображает отношения между суждениями? Почему логический квадрат не изображает отношение равнозначности? Как с помощью логического квадрата определять отношение между двумя простыми сравнимыми суждениями?
6. Возьмите какое-нибудь истинное или ложное суждения вида A и сделайте из него выводы об истинности сравнимых с ним суждений видов E, I, O. Возьмите какое-нибудь истинное или ложное суждения вида E и сделайте из него выводы об истинности сравнимых с ним суждений A, I, O.
2.6. Сложное суждение
В зависимости от союза, с помощью которого простые суждения соединяются в сложные, выделяется пять видов сложных суждений:
1. Конъюнктивное суждение (конъюнкция) – это сложное суждение с соединительным союзом "и", который обозначается в логике условным знаком "∧". С помощью этого знака конъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы: a ∧ b (читается "a и b"), где a и b – это два каких-либо простых суждения. Например, сложное суждение: "Сверкнула молния, и загремел гром", – является конъюнкцией (соединением) двух простых суждений: "Сверкнула молния", "Загремел гром". Конъюнкция может состоять не только из двух, но и из большего числа простых суждений. Например: "Сверкнула молния, и загремел гром, и пошёл дождь (a ∧ b ∧ c)".
2. Дизъюнктивное суждение(дизъюнкция) – это сложное суждение с разделительным союзом "или". Вспомним, что, говоря о логических операциях сложения и умножения понятий, мы отмечали неоднозначность этого союза – он может использоваться как в нестрогом (неисключающем) значении, так и в строгом (исключающем). Неудивительно поэтому, что дизъюнктивные суждения делятся на два вида:
1. Нестрогая дизъюнкция – это сложное суждение с разделительным союзом "или" в его нестрогом (неисключающем) значении, который обозначается условным знаком "∨". С помощью этого знака нестрогое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы: a ∨ b (читается "a или b"), где a и b – это два простых суждения. Например, сложное суждение: "Он изучает английский, или он изучает немецкий", – является нестрогой дизъюнкцией (разделением) двух простых суждений: "Он изучает английский", "Он изучает немецкий". Эти суждения друг друга не исключают, ведь возможно изучать и английский, и немецкий одновременно, поэтому данная дизъюнкция является нестрогой.
2. Строгая дизъюнкция – это сложное суждение с разделительным союзом "или" в его строгом (исключающем) значении, который обозначается условным знаком "
". С помощью этого знака строгое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы: ab (читается "или a, или b"), где a и b – это два простых суждения. Например, сложное суждение: "Он учится в 9 классе, или он учится в 11 классе", – является строгой дизъюнкцией (разделением) двух простых суждений: "Он учится в 9 классе", "Он учится в 11 классе". Обратим внимание на то, что эти суждения друг друга исключают, ведь невозможно одновременно учиться и в 9, и в 11 классе (если он учится в 9 классе, то точно не учится в 11 классе, и наоборот), в силу чего данная дизъюнкция является строгой.
Как нестрогая, так и строгая дизъюнкции могут состоять не только из двух, но и из большего числа простых суждений. Например: "Он изучает английский, или он изучает немецкий, или он изучает французский (a ∨ b ∨ c)", "Он учится в 9 классе, или он учится в 10 классе, или он учится в 11 классе (a b c)".
3. Импликативное суждение(импликация) – это сложное суждение с условным союзом "если … то", который обозначается условным знаком "→". С помощью этого знака импликативное суждение, состоящее из двух простых суждений, можно представить в виде формулы: a → b (читается "если a, то b"), где a и b – это два простых суждения. Например, сложное суждение: "Если вещество является металлом, то оно электропроводно", – представляет собой импликативное суждение (причинно-следственную связь) двух простых суждений: "Вещество является металлом", "Вещество электропроводно". В данном случае эти два суждения связаны таким образом, что из первого вытекает второе (если вещество – металл, то оно обязательно электропроводно), однако из второго не вытекает первое (если вещество электропроводно, то это вовсе не означает, что оно является металлом). Первая часть импликации называется основанием, а вторая – следствием; из основания вытекает следствие, но из следствия не вытекает основание. Формулу импликации: a → b, можно прочитать так: "если a, то обязательно b, но если b, то не обязательно a".