32. Для большей определенности рассмотрим случай, когда расходящиеся лучи, испускаемые одной и той же светящейся точкой, отражаются от двух слегка наклоненных друг к другу зеркал таким образом, что получаются два пучка лучей, сходящихся под заметным углом; тогда обе системы световых волн, отраженных от этих зеркал, пересекаются под тем же углом, и это легкое наклонение имеет следствием, что если в какой-нибудь точке одна полуволна первой системы точно совпадает с полуволной второй системы, толкающей жидкость в том же направлении, то налево и направо от этой точки пересечения совпадения не будет, но немного дальше оно произойдет опять – с одной стороны с полуволной предшествующего противоположного движения, а с другой стороны – с полуволной последующего. Потом совпадения опять не будет, но затем на двойном расстоянии от первого совпадения полуволна первой системы опять совпадет с двумя полуволнами, импульсы которых действуют в ту же сторону, как и ее собственный; отсюда следует, что на поверхности этой волны появится ряд равноотстоящих линий, в которых движение по очереди усиливается волнами другого пучка. Таким образом, если заставить падать эту световую волну на белый картон, то на нем должен быть виден ряд темных и блестящих полос, если свет приблизительно однороден, или же ряд окрашенных в разные цвета полос, если пользуются белым светом.
Только что нами сказанное станет более понятным с помощью рисунка; он представляет сечение двух зеркал и отраженных волн, сделанное плоскостью, проведенной через светящуюся точку перпендикулярно к зеркалам, которые проектируются по ED и DF.
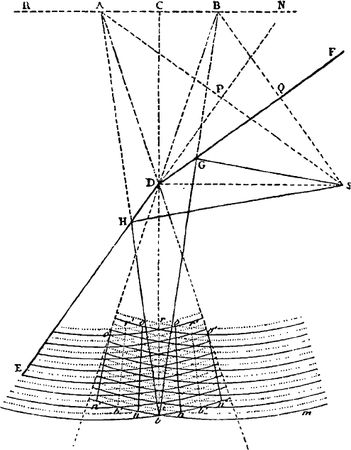
Рис. 70
Пусть светящаяся точка будет в S и пусть А и В представляют геометрические положения ее двух изображений, которые определяют, опустив из точки S на два зеркала ED и DF перпендикуляры SA и SB и взяв РА равным SP и QB равным SQ; в самом деле, к определенным таким способом точкам А и В будут, по известным законам отражения, сходиться лучи, отраженные от первого и второго зеркал. Таким образом, чтобы получить, например, в какой-нибудь точке G зеркала DF направление отраженного луча, достаточно провести прямую через В и G, и продолжение этой прямой будет отраженным лучом. Но следует заметить, что по построению, которое нам дало точку В, расстояния BG и SG одинаковы и что, таким образом, весь путь, пройденный световым лучом от точки S до точки b, совершенно такой же, как если бы он исходил от точки В. Это геометрическое следствие приложимо ко всем лучам, отраженным от одного и того же зеркала, и мы видим, что все они должны приходить в одно и то же время к различным точкам окружности п'bт, описанной из B как центра радиусом, равным Bb. Эта окружность представляет собой, значит, поверхность отраженной волны, пришедшей в b, или, говоря точнее, пересечение этой поверхности с плоскостью рисунка. Подобным же образом волны, отраженные от зеркала, будут иметь свой центр в А.
Чтобы изобразить обе системы волн, отраженных из точек А и В как из центров, опишем ряд равноотстоящих друг от друга дуг, промежутки между которыми предполагаются равными одной полуволне. Для того чтобы можно было различить противоположные движения, дуги окружностей изображены сплошными штрихами, если предполагается, что в рассматриваемый момент эфирные молекулы обладают в них наибольшей скоростью вперед, и пунктирной линией, если предполагается, что эфирные молекулы обладают в них наибольшей скоростью назад. Отсюда следует, что пересечения пунктирных дуг окружностей со сплошными представляют собой точки полной противоположности движения и, следовательно, середины темных полос; напротив, пересечения одинаковых дуг дают точки полной согласованности движения, т. е. середины блестящих полос. Пунктирными линиями br, b'r', b'r и т. д. соединены соответствующие пересечения дуг одного и того же рода и сплошными линиями no, no, n'o', n'o' и т. д. пересечения дуг различных родов; первые из них дают последовательные положения, или траектории середин темных полос, а вторые – середин блестящих полос.
В этом рисунке мы были вынуждены увеличить в огромное число раз действительную длину световых волн и преувеличить взаимный наклон обоих зеркал. Таким образом, в нем не нужно искать точного изображения действительности, но только способ изобразить игру интерференции в волнах, пересекающихся под заметным углом.
С помощью очень простых геометрических рассуждений легко видеть, что ширина полос обратно пропорциональна величине угла, который образуют между собой оба интерферирующих пучка, и что промежуток, заключенный между серединами двух последовательных темных или блестящих полос, равен длине волны, разделенной на синус угла, под которым пересекаются лучи. В самом деле, треугольник bni, образованный прямой линией bi и двумя дугами круга ni и nb, можно рассматривать вследствие малости этих дуг как прямолинейный и равнобедренный, синус же угла bni в виду его малости будет приблизительно равен ib/bn; значит, bn равно ib, разделенному на этот синус. Но стороны угла bni перпендикулярны к сторонам угла AbB, так как bn перпендикулярно к Ab и ni к Bb; значит, эти углы равны между собой, и один из них можно подставить вместо другого; таким образом, изобразив через i угол AbB, под которым пересекаются отраженные лучи, имеем:
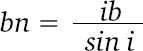
значит, nn, которое в два раза больше, чем bn, будет равно 2ib / sin i. Но nn представляет собой расстояние между серединами двух последовательных темных полос и является, следовательно, тем, что мы назвали шириною полосы; так как по построению чертежа ib есть длина полуволны, то 2ib будет длиною целой волны; значит, ширина полосы действительно равна длине волны, разделенной на синус угла, который образуют между собой отраженные лучи и который в то же время будет углом, под которым виден промежуток АВ между двумя изображениями светящейся точки, если поместить глаз в b.
Можно найти другую формулу, равносильную этой, если заметить, что два треугольника bni и AbB подобны, что дает пропорцию:
bn: bi = Ab: АВ,
откуда следует
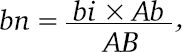
или