
Рис. 6
Вращая треугольники, из которых составлен правильный шестиугольник, мы получаем 18 различных разновидностей шестиугольников. Если гексагексафлексагон сделан из прямой полоски бумаги, то три из этих 18 шестиугольников никогда не встретятся нам, как бы мы ни складывали наш флексагон. Это навело одного из наших читателей на мысль наклеить на каждый разворот гексафлексагона части трех различных картинок. Перегибая определенным образом флексагон, мы будем видеть по очереди в центре открывшейся поверхности одну из картинок, а на периферии - фрагменты двух других изображений. К трем "скрытым" шестиугольникам, которые никогда полностью не появляются на видимой стороне флексагона, он приклеил разрезанные на части портреты трех очаровательных девушек, которых зритель, несмотря на все свои старания, никак не может рассмотреть во всех подробностях.
Свою игрушку читатель назвал гексагексафрастрагоном. Другой читатель добился аналогичных результатов, склеив два смежных треугольника. Из-за этого исчез целый шестиугольник, и жертвы невинного розыгрыша тщетно пытались найти недостающий разворот флексагона. Неудача казалась тем более непонятной, что, заглянув внутрь флексагона, они собственными глазами видели части таинственно исчезнувшей поверхности!
Утверждение о том, что шестиугольники, возникающие при развороте гексагексафлексагонов, могут быть только 15 различных типов, необходимо несколько уточнить. Несимметричная раскраска поверхностей гексагексафлексагонов позволяет обнаружить любопытный факт: три из 15 допустимых шестиугольников имеют свои зеркально-симметричные пары. Перенумеровав внутренние углы каждого из допустимых шестиугольников по часовой стрелке цифрами от 1 до 6, мы обнаружим, что при складывании флексагонов три шестиугольника переходят в зеркально-симметричные шестиугольники, у которых углы перенумерованы теми же цифрами, но расположенными в обратном порядке. Если принять во внимание эту асимметрию, то можно сказать, что шесть поверхностей гексафлексагона могут порождать 18 различных шестиугольников.
Для тех, кто захочет сам изготовить флексагоны других типов, отличные от рассмотренных, мы приводим краткий обзор флексагонов низших порядков.
1. Унагексафлексагон . Полоску из трех треугольников разглаживают и концы ее соединяют так, чтобы получился лист Мёбиуса с треугольным краем (более изящная модель листа Мёбиуса с треугольным краем рассматривается в главе 7). Поскольку лист Мёбиуса имеет только одну сторону и состоит из шести треугольников, его можно назвать унагексафлексагоном, хотя, разумеется, у него нет шести сторон и он не складывается.
2. Дуогексафлексагон представляет собой просто шестиугольник, вырезанный из бумаги. У него две стороны, но он не складывается.
3. Тригексафлексагон. Существует только одна разновидность этого флексагона, именно она и была уже описана нами.
4. Тетрагексафлексагон также существует лишь в единственном варианте. Его складывают из пилообразной полоски, изображенной на рис. 7а.

5. Пентагексафлексагон. Единственную разновидность этого флексагона складывают из полоски, показанной на рис. 7б.
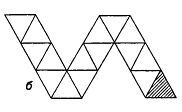
6. Гексагексафлексагон. Существует три различных типа этих флексагонов, каждый из них обладает неповторимыми свойствами. Мы дали описание лишь одного типа. Два остальных можно сделать из полосок, форма которых показана на рис. 7 в.
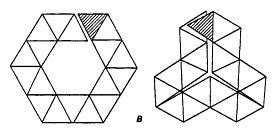
7. Гептагексафлексагон. Его складывают из трех полосок бумаги, изображенных на рис. 7 г.
Первую полоску можно сложить двумя различными способами, поэтому общее число возможных форм гептагексафлексагонов равно 4. Третью форму этих флексатонов конструируют из полоски бумаги, имеющей вид восьмерки с перекрывающимися частями. Это первая из фигур, которые Луи Таккерман назвал "флексагонными улицами". Поверхности этой фигуры можно перенумеровать так, что на "пути Таккермана" они будут встречаться "по порядку номеров", как дома на улице.
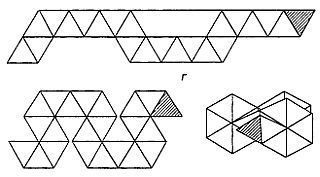
Рис. 7 Зигзагообразные полоски бумаги для складывания гексафлексагонов. Заштрихованные треугольники служат клапанами для склеивания.
Существует 12 различных типов октагексафлексагонов, 27 типов эннагексафлексагонов и 82 типа декагексафлексагонов. Точное число флексагонов каждого порядка определяется неоднозначно и зависит от того, что следует понимать под "различными" флексагонами. Например, все флексагоны имеют асимметричную структуру и делятся на правые и левые, но зеркально-симметричные формы флексагонов вряд ли следует считать самостоятельными. Более подробно о числе неэквивалентных флексагонов каждого порядка можно прочитать в статье Оукли и Визнера.
Порядки гексафлексагонов, которые можно сложить из прямых полосок, поделенных на равносторонние треугольники, всегда кратны трем. Особенно легко построить одну разновидность гексафлексагонов с двенадцатью поверхностями. Для этого берут прямую полоску бумаги вдвое длиннее той, из которой мы складывали гексагексафлексагон, и "скручивают" ее так, как показано на рис. 2б.
При этом длина полоски сократится вдвое и станет равной длине гексагексафлексагонной полоски. Затем скрученную полоску нужно сложить точно таким образом, как если бы вы складывали гексагексафлексагон. В результате получится додекагексафлексагон.
Экспериментируя с флексагонами высоких порядков, полезно иметь в виду удобное правило: число слоев бумаги в двух соседних треугольных секциях всегда равно числу поверхностей данного флексагона. Интересно также отметить, что если каждую поверхность флексагона пометить каким-нибудь числом или символом и этот символ поставить на всех треугольниках, принадлежащих данной поверхности, то чередование символов на развернутой полоске будет обладать трехкратной периодичностью. Например, на лицевой и обратной сторонах развертки гексагексафлексагона, изображенного на рис. 2, цифры будут располагаться в такой последовательности: