Неудобства начинались при обращении с дробями: ведь точку не раздробишь на части. Поэтому греки предпочитали иметь дело не с дробями, а с отношениями: говорили не "одна седьмая часть единицы", а "одна единица от семи". Отношения и пропорции они сортировали с большой любовью. Мы говорим: "Число 20 кратно числу 5", то есть делится на него. А грек мог вдобавок сказать: "Число 20 кратночастно числу 16", то есть делится на разность между ними. Вы знаете: число 4 – это среднее арифметическое чисел 2 и 6, то есть сумма их, деленная пополам. Некоторые, может быть, знают: число 4 – это среднее геометрическое чисел 2 и 8, то есть квадратный корень из их произведения. А грек вдобавок знал: число 4 – это "среднее гармоническое" чисел 3 и 6, то есть их удвоенное произведение, деленное на их сумму.
Когда вы начинали учить алгебру, то заучивали такие формулы, как:
(a + b) = a + 2ab + b;
(a – b) = a – 2ab + b;
a – b = (a + b) (a – b).
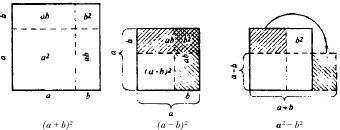
Вы помните, как они выводились? Это было довольно громоздко. А грек со своей привычкой к наглядности доказывал их не вычислением, а чертежом: чертил отрезок А, отрезок В, строил на них квадраты и показывал: "Вот!" Посмотрите и убедитесь.
Такие геометрические доказательства выручали греков в их страхе перед бесконечностью. Вы смогли бы, например, извлечь точный корень из числа 2? Нет, не смогли бы: получили бы бесконечную дробь. А греческий математик поступал просто: чертил отрезок длиной в данное число, строил вокруг квадрат, в котором он был бы диагональю, показывал на сторону этого квадрата и говорил: "Вот!"
В современной математике такие величины, никогда не вычисляемые до конца, называются иррациональными. Греки называли их "невыразимые". "Невыразимым" было отношение диагонали и стороны в квадрате– 1,41421…; "невыразимым" было и отношение длины окружности к диаметру в круге, знаменитое число "пи" – 3,14159… (π – это первая буква греческого слова "периферия", окружность). Это число изобразить было труднее, и греческие математики в своей борьбе с бесконечностью век за веком ломали голову над "квадратурой круга": как по данному диаметру крута с помощью только циркуля и линейки построить квадрат, равновеликий этому кругу?
Можно задать вопрос: а почему, собственно, с помощью только циркуля и линейки? Не попробовать ли изобрести новый прибор, посложнее, который позволил бы решить эту задачу? Но грек нам гордо ответил бы: "Возиться с приборами – это дело раба, привычного к ручному труду, а свободному человеку приличествует полагаться лишь на силу ума".
Вот как, оказывается, рабовладельческий образ мысли проявляется даже в такой отвлеченной науке, как математика.
Четыре стихии
Гераклита и Парменида решил помирить сицилиец Эмпедокл. Он сказал: "Ни война, ни мир на земле не вечны. Так и во вселенной. Они сменяют друг друга, как времена года. Мир шарообразен, но этот шар неоднороден. В нем смешаны четыре стихии: земля, вода, воздух, огонь. А над ними властвуют две силы: Любовь и Вражда. Наступает пора мира – и в центре мирового шара царствует Любовь, она сливает вокруг себя четыре стихии в то самое Единство, о котором мечтал Парменид, а Вражда отступает и лишь снаружи облегает мировой шар. Наступает новая пора – и Вражда со всех сторон начинает проникать в мир, вытесняя из него Любовь, а на пути своем она разобщает четыре стихии, и они встают войной друг на друга. Наконец Вражда восседает в центре мира, вокруг нее кипит гераклитовская война четырех стихий, а Любовь оттеснена наружу и ждет своего часа. А потом все повторяется в обратном порядке. Если это на что-нибудь похоже, то больше всего – на гражданский мир и гражданскую войну в городе, где есть несколько политических партий. Сейчас мир на полпути: то ли от Вражды к Любви, то ли наоборот".
Как Фемистоклу не давали спать лавры Мильтиада, так Эмпедоклу – лавры Пифагора. Он тоже хотел быть пророком и чудотворцем. Когда ему предложили царскую власть, он отверг ее: "Лучшее из растений – лавр, из животных – лев, из людей – мудрец, а вовсе не царь". Держался он еще величавее, чем царь, носил пурпурный плащ, золотую повязку на голове и медные сандалии. Учение свое он изложил стихами и читал эти стихи в Олимпии. А когда в Олимпии его колесница одержала победу на играх, он принес в жертву быка из медового теста и пряностей, потому что пифагорейский закон запрещал убивать животных.
В одном городе люди часто болели оттого, что вода в реке была нездоровой. Эмпедокл провел к ней канал от другой реки, и болезни прекратились. В другом городе вода была здоровой, а люди все равно болели. Эмпедокл догадался, что это оттого, что ветры, дующие на город из-за гор, были нездоровыми; он приказал загородить бычьими кожами ущелья в горах, и болезни прекратились. С этих пор его прозвали "ветроловом". В этом был не только восторг перед его проницательностью, но и насмешка над его тщеславной погоней за почестями. Тщеславен он был до крайности и считал, что равных ему нет на свете. Однажды он сказал Пармениду: "Трудно найти истинного философа!" – "Да, – невозмутимо ответил Парменид, – для этого надо самому быть истинным философом".
Он не хотел умирать, как все люди, а хотел сжечь себя, как Геракл, чтобы сделаться богом. Почувствовав приближение смерти, он вскарабкался на огнедышащую Этну и бросился в ее жерло. Лава выбросила на склон его медную сандалию.
Учение о четырех стихиях Эмпедокл перенял от пифагорейцев. Он рассуждал, как из них строится мироздание, а его современник Алкмеон, тоже пифагореец, рассуждал, как из них строится человеческое тело. В нем четыре жизненных сока: кровь, слизь, желтая желчь и черная желчь. Если между ними равновесие, "равнозаконие", как в хорошем государстве, – человек здоров; если оно нарушено – человек болен. Душевные свойства человека тоже зависят от смешения четырех соков (смешение – по-латыни "темперамент"; может быть, вы слышали это слово). Основных темпераментов – четыре: бодрый – сангвиник, вялый – флегматик, вспыльчивый – холерик, мрачный – меланхолик. Имена эти значат: "кровник", "слизевик", "желчевик" и "черножелчевик"; понятия эти до сих пор употребляются в психологии.
Сто лет спустя в Эмпедокловой четверке тасующихся стихий навел покой и порядок Аристотель. Как он это сделал, мы узнаем после. Самое же любопытное – то, что этими понятиями пользуется и современная наука, только по-другому их называет. Если бы Эмпедокл услышал, как мы говорим: "Есть четыре состояния вещества: твердое, жидкое, газообразное и плазма", – он узнал бы в них свои четыре стихии.
Смеющийся философ
Как современная физика вспоминает таким образом порой о четырех стихиях Эмпедокла, так современная химия – об атомах Демокрита.
У Эмпедокла картина мира была похожа на картину города, раздираемого борьбой четырех партий. Демокрит спросил себя: а откуда берутся сами эти партии? В городе – это понятно: люди сходных мыслей случайно встречаются, знакомятся, начинают держаться вместе, к ним присоединяются новые и новые, и так возникает целое большое общество.
Может быть, так же устроен и мир? Он состоит из частиц, мелких до невидимости и густо носящихся в пустоте, как пылинки в солнечном луче. С течением времени они начинают как бы сортироваться: крупные к крупным, круглые к круглым, треугольные к треугольным. (Почему? Насыпьте на блюдо песок и потрясите: крупные песчинки выйдут наверх, мелкие останутся внизу. Вот так же и мировые частицы.) Так образуются сперва четыре стихии: из крупных частиц – земля, из круглых – огонь и так далее, а потом – отдельные вещи.
Мы не можем видеть эти частицы, но мы их чувствуем: если в теле, например, много гладких частиц, оно кажется глазу светлым, а вкусу сладким. Поэтому не надо, как Парменид, говорить, что мир, ощущаемый нами, – "ненастоящий", и не надо, как Гераклит, горевать, что наш ум не угонится за его изменчивостью. Нужно только быть внимательным и вдумчивым – и мир поддастся изучению.
Попутно такое рассуждение давало ответ и на задачу Зенона об Ахилле и черепахе. Зенон говорил: "Раз нет в мире бесконечного деления – значит, нет никакого деления, значит, есть только неделимое Единство". А мы лучше скажем: раз нет бесконечного деления – значит, есть деление конечное, вплоть до таких мелких частиц, разделить которые уже невозможно. Государство мы разделили на партии, партии – на людей, но людей-то мы уже делить не можем: полчеловека ни в какую партию не годятся. Так и в мироздании: все можно делить, пока не получатся наши частицы-пылинки, а их уже не разделишь. Демокрит так и называл эти частицы: "неделимые" – по-гречески "атомы".
Как же будет выглядеть погоня Ахилла за черепахой? Сперва Ахилл будет делать широкие шаги, потом – в угоду Зенону – все более мелкие, чтобы покрыть сперва половину расстояния до черепахи, потом половину половины и так далее и наконец сделает такой маленький шажок, что меньше уже никак нельзя сделать, а можно только повторить такой же. Вот тут-то все и кончится: этим следующим шагом Ахилл обгонит черепаху – и здравый смысл восторжествует.