Всего за 133 руб. Купить полную версию
15. Входной язык содержит операторы условия типа if… then… else и if… then, разделенные символом; (точка с запятой). Операторы условия содержат идентификаторы, знаки сравнения <, >, =, строковые константы (последовательность символов в двойных кавычках), знак присваивания (:=).
16. Входной язык содержит операторы цикла типа for (…;…;…) do, разделенные символом; (точка с запятой). Операторы цикла содержат идентификаторы, знаки сравнения <, >, =, строковые константы (последовательность символов в двойных кавычках), знак присваивания (:=).
Примечание.
• Римскими числами считать последовательности заглавных латинских букв X, V и I;
• шестнадцатеричными числами считать последовательность цифр и символов "а", "Ь", "с", "d, "е" и "f", начинающуюся с цифры (например: 89, 45ас9, 0abc4);
• задание по лабораторной работе № 2 взаимосвязано с заданием по лабораторной работе № 3, для уточнения состава входного языка можно посмотреть грамматику, заданную в работе № 3 по соответствующему варианту.
Пример выполнения работы
Задание для примера
В качестве задания для примера возьмем входной язык, который содержит набор условных операторов условия типа if… then… else и if… then, разделенных символом; (точка с запятой). Эти операторы в качестве условия содержат логические выражения, построенные с помощью операций or, xor и and, операндами которых являются идентификаторы и целые десятичные константы без знака. В исполнительной части эти операторы содержат или оператор присваивания переменной логического выражения (:=), или другой условный оператор.
Комментарий будет организован в виде последовательности символов, начинающейся с открывающей фигурной скобки ({) и заканчивающейся закрывающей фигурной скобкой (}). Комментарий может содержать любые алфавитно-цифровые символы, в том числе и символы национальных алфавитов.
Грамматика входного языка
Описанный выше входной язык может быть построен с помощью КС-грамматики G({if,then,else,a,=,or,xor,and,(,),},{S,F,E,D,C},P,S) с правилами Р:
S → F;
F → if E then T else F | if E then F | a:= E
T → if E then T else T | a:= E
E → E or D | E xor D | D
D → D and С | С
С → a | (E)
Описание грамматики построено в форме Бэкуса-Наура. Жирным шрифтом в грамматике и в правилах выделены терминальные символы.
Выбранный в качестве примера язык и задающая его грамматика не совпадают ни с одним из предложенных выше вариантов. С другой стороны, на этом примере можно проиллюстрировать многие особенности построения лексического, а впоследствии – и синтаксического распознавателя, присущие различным вариантам. Он содержит как условные операторы, связанные с передачей управления в то или иное место исходной программы, так и линейные операции в форме вычисления логических выражений. Поэтому данный пример выбран в качестве иллюстрации для лабораторной работы № 2, а позже будет использоваться также в лабораторных работах № 3 и 4.
Описание конечного автомата для распознавания лексем входного языка
Задача лексического анализатора для описанного выше языка заключается в том, чтобы распознавать и выделять в исходном тексте программы все лексемы этого языка. Лексемами данного языка являются:
• шесть ключевых слов языка (if, then, else, or, xor и and);
• разделители: открывающая и закрывающая круглые скобки, точка с запятой;
• знак операции присваивания;
• идентификаторы;
• целые десятичные константы без знака.
Кроме перечисленных лексем распознаватель должен уметь определять и исключать из входного текста комментарии, принцип построения которых описан выше. Для выделения комментариев ключевыми символами должны быть открывающая и закрывающая фигурные скобки.
Для перечисленных типов лексем и комментария можно построить регулярную грамматику, а затем на ее основе создать КА. Однако построенная таким образом грамматика, с одной стороны, будет элементарно простой, с другой стороны – громоздкой и малоинформативной. Поэтому можно пойти путем построения КА непосредственно по описанию лексем. Для этого не хватает только описания идентификаторов и целых десятичных констант без знака:
• идентификатор – это произвольная последовательность малых и прописных букв латинского алфавита (от А до Z и от а до z), цифр (от 0 до 9) и знака подчеркивания (_), начинающаяся с буквы или со знака подчеркивания;
• целое десятичное число без знака – это произвольная последовательность цифр (от 0 до 9), начинающаяся с любой цифры.
Границами лексем для данного распознавателя будут служить пробел, знак табуляции, знаки перевода строки и возврата каретки, а также круглые скобки, открывающая фигурная скобка, точка с запятой и знак двоеточия. При этом следует помнить, что круглые скобки и точка с запятой сами по себе являются лексемами, открывающая фигурная скобка начинает комментарий, а знак двоеточия, являясь границей лексемы, в то же время является и началом другой лексемы – операции присваивания.
В данном языке лексический анализатор всегда может однозначно определить границы лексемы, поэтому нет необходимости в его взаимодействии с синтаксическим анализатором и другими элементами компилятора.
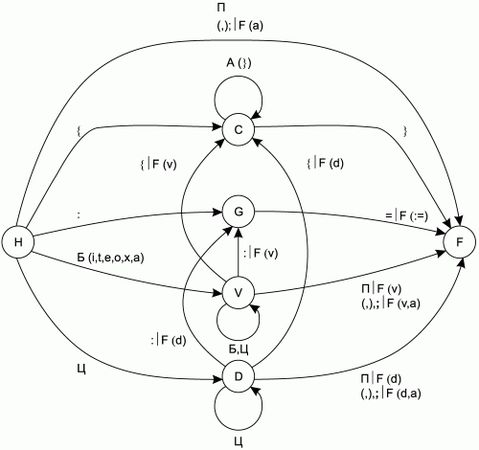
Рис. 2.1. Фрагмент графа переходов КА для распознавания всех лексем, кроме ключевых слов.
Полный граф переходов КА будет очень громоздким и неудобным для просмотра, поэтому проиллюстрируем его несколькими фрагментами. На рис. 2.1 изображен фрагмент графа переходов КА, отвечающий за распознавание разделителей, комментариев, знака присваивания, переменных и констант (всех лексем входного языка, кроме ключевых слов).
На рис. 2.2 изображен фрагмент графа переходов КА, отвечающий за распознавание ключевых слов if и then (этот фрагмент имеет ссылки на состояния, изображенные на рис. 2.1). Аналогичные фрагменты можно построить и для других ключевых слов.
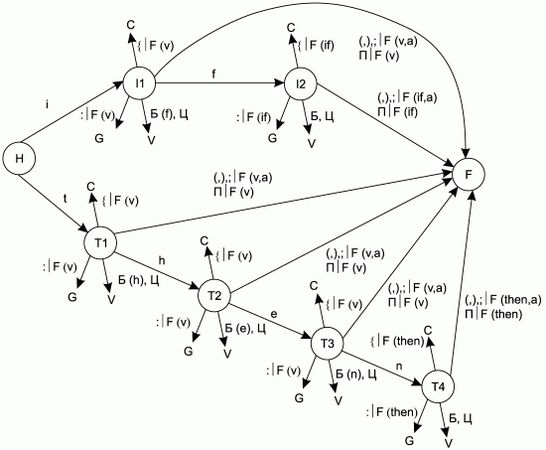
Рис. 2.2. Фрагмент графа переходов КА для ключевых слов if и then.
На фрагментах графа переходов КА, изображенных на рис. 2.1 и 2.2, приняты следующие обозначения:
• А– любой алфавитно-цифровой символ;
• А(*) – любой алфавитно-цифровой символ, кроме перечисленных в скобках;
• П– любой незначащий символ (пробел, знак табуляции, перевод строки, возврат каретки);
• Б– любая буква английского алфавита (прописная или строчная) или символ подчеркивания (_);
• Б(*) – любая буква английского алфавита (прописная или строчная) или символ подчеркивания (_), кроме перечисленных в скобках;
• Ц– любая цифра от 0 до 9;
• F – функция обработки таблицы лексем, вызываемая при переходе КА из одного состояния в другое. Обозначения ее аргументов:
– v – переменная, запомненная при работе КА;
– d – константа, запомненная при работе КА;
– a – текущий входной символ КА.
С учетом этих обозначений, полностью КА можно описать следующим образом:
M(Q,Σ,δ,q0,F):
Q = {H, C, G, V, D, I1, I2, T1, T2, T3, T4, E1, E2, E3, E4, O1, O2, X1, X2, X3, A1, A2, A3, F}
Σ = А (все допустимые алфавитно-цифровые символы);
q 0 = H;
F = {F}.
Функция переходов (δ) для этого КА приведена в приложении 2.
Из начального состояния КА литеры "i", "t", "e", "o", "x" и "a" ведут в начало цепочек состояний, каждая из которых соответствует ключевому слову:
• состояния I1, I2 – ключевому слову if;
• состояния T1, T2, T3, T4 – ключевому слову then;
• состояния E1, E2, E3, E4 – ключевому слову else;
• состояния O1, O2 – ключевому слову or;
• состояния X1, X2, X3 – ключевому слову xor;
• состояния A1, A2, A3 – ключевому слову and.
Остальные литеры ведут к состоянию, соответствующему переменной (идентификатору), – V. Если в какой-то из цепочек встречается литера, не соответствующая ключевому слову, или цифра, то КА также переходит в состояние V, а если встречается граница лексемы – запоминает уже прочитанную часть ключевого слова как переменную (чтобы правильно выделять такие идентификаторы, как "i" или "els", которые совпадают с началом ключевых слов).
Цифры ведут в состояние, соответствующее входной константе, – D. Открывающая фигурная скобка ведет в состояние C, которое соответствует обнаружению комментария – из этого состояния КА выходит, только если получит на вход закрывающую фигурную скобку. Еще одно состояние – G – соответствует лексеме "знак присваивания". В него КА переходит, получив на вход двоеточие, и ожидает в этом состоянии символа "равенство".
Состояние H – начальное состояние КА, а состояние F – его конечное состояние. Поскольку КА работает с непрерывным потоком лексем, перейдя в конечное состояние, он тут же должен возвращаться в начальное, чтобы распознавать очередную лексему. Поэтому в моделирующей программе эти два состояния можно объединить.
На графе и при описании функции переходов не обозначено состояние "ошибка", чтобы не загромождать и без того сложный граф и функцию. В это состояние КА переходит всегда, когда получает на вход символ, по которому нет переходов из текущего состояния.