На дереве видны многочисленные ветви, в каждой из которых – свой общий предок. Нет и не может быть в такой ситуации некоего "одного общего предка", ветви нужно анализировать раздельно. Как было показано в наших работах, серия идентичных гаплотипов, идущих по кругу выше, имеют общего предка, который жил 1075±130 лет назад ("академическая выборка") или 1050±190 лет назад ("коммерческая выборка", то есть по коммерческим базам данных), что практически одно и то же, и разница между ними заметно проявляется уже в 67-маркерном формате гаплотипов.
Какой вывод из этого следует? Тот, что нельзя проводить расчеты по сериям гаплотипов "чохом", без разделения их на ветви. Нет ничего проще, чем выписать гаплотипы в серию, посчитать в них мутации от чего-то среднего, или от какого-то заранее заданного "предкового" гаплотипа, и разделить число мутаций на число гаплотипов и на скорость мутаций, которая нравится, или почему-то принимается. Какое-то число при этом всегда получится. Но это будет, как правило, мусор, с претензией на "научность". Популяционные генетики заполняют подобным мусором академические журналы на протяжении последних 20 лет. Никакого смысла в этих "расчетах" нет.
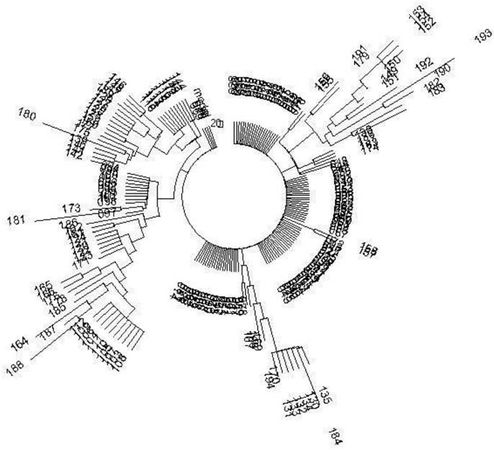
Рис. 13. Дерево 6-маркерных гаплотипов евреев гаплогруппы J, построено по данным Behar et al. (2003). В выборке – 194 гаплотипа.
Но как узнать, рассматриваемая серия гаплотипов "однородная", от одного общего предка, или разнородная, от разных общих предков, и дальнейшие расчеты в таком виде бессмысленны? Это – важный, и даже важнейший вопрос, который в ДНК-генеалогии решается двумя путями – графическим и аналитическим. Графический метод – это постройка дерева гаплотипов и его рассмотрение, симметричное ли дерево, или состоит из различных ветвей. Если симметричное (примеры даны ниже), то можно применять простые метода расчета, как линейный или с помощью калькулятора Килина-Клёсова. Если дерево состоит из четко разделяющихся ветвей, как на рис. 13, то расчеты (линейный или калькуляторный) следует проводить по каждой ветви раздельно.
Аналитический метод – это применение логарифмического метода анализа гаплотипов, и полученный результат (число лет до общего предка) сравнивается с результатом линейного расчетного метода, применяемого "чохом", ко всей серии гаплотипов. Если результаты различаются (пример дан ниже), то серия гаплотипов неоднородна, и надо переходить к графическому методу разделения ветвей, как описано выше.
Например, в ситуации с 194 гаплотипами евреев гаплогруппы J (рис. 13), линейный метод ("чохом") дает 263/194/0.0074, и получается 5600±660 лет до общего предка "гаплотипов коэнов". Логарифмический метод дает [ln(194/91)/0.0074] = 102 → 114 условных поколений, или 2850±410 лет до общего предка. Результаты совершенно разные, значит, ни тот ни другой метод не подходят. Собственно, это и показывает рис. 13.
Вот этого попгенетики никогда не могли усвоить.
Вопрос 72: Можно несколько подробнее о линейном методе расчета?
Как было неоднократно объяснено выше, линейный метод – самый простой при вычислении времени, прошедшего от общего предка данной серии гаплотипов. Поскольку чем больше это время, тем больше мутаций накопилось в гаплотипах потомков общего предка, и мутации в гаплотипах накапливаются в основном неупорядоченно, то к расчетам применима простая формула:
n/N = kt,
где n – число мутаций в серии гаплотипов, N – число гаплотипов в серии, k – константа скорости мутации, t – время до ближайшего общего предка.
Пояснения: (1) число мутаций считается от базового гаплотипа, который или является предковым, или максимально к нему приближен, насколько позволяет подборка гаплотипов, (2) отношение числа мутаций к числу гаплотипов определяет произведение kt, которое выражается в числе мутаций; как видно, константа в таких формулах всегда связана со временем до общего предка, (3) время до общего предка обычно определяют в условных поколениях протяженностью 25 лет, и тогда константа скорости мутациях определяется в числе мутаций на условное поколение протяженностью в 25 лет. Как видно, извечный вопрос попгенетиков о том, какую протяженность поколения использовать в расчетах, лишен смысла, поскольку какую протяженность мы бы ни брали, она входит в величину константы скорости мутаций, и итоговая величина kt остается той же, равной отношению n/N. А это – независимая переменная, она задается серией гаплотипов, то есть независимой выборкой. "Независимой" здесь означает, что гаплотипы для выборки не подбираются по усмотрению исследователя, они выбираются неупорядоченно.
Пример: имеются 275 111-маркерных гаплотипов гаплогруппы N1C1. В них суммарно имеются 6270 мутаций. Общий предок жил 6270/275/0.198 = 115 → 130 условных поколения, или 3250±330 лет назад (округленно). Калькулятор Килина-Клёсова дал 3233±326 лет назад.
Поправка на возвратные мутации производится или по специальным таблицам, , или по формуле, приведенной в этой книге выше.
Вопрос 73: Можно подробнее о квадратичном (пермутационном) методе, и расчете погрешностей при его использовании?
Квадратичный метод, в отличие от линейного, есть в двух основных вариантах – с использованием базового гаплотипа и без ориентации на базовый гаплотип. В первом случае считаются не мутации от базового гаплотипа, а квадраты мутаций. Например, в серии из трех 12-маркерных гаплотипов
13 24 16 10 11 15 12 12 10 13 11 30
13 25 16 11 11 15 12 12 10 13 11 30
13 24 16 11 11 15 12 12 11 13 11 30
с базовым гаплотипом
13 24 16 11 11 15 12 12 10 13 11 30
и тремя мутациями от базового гаплотипа (выделены), линейный метод дает 3/3/0.02 = 50 → 53 условных поколения, то есть 1325±780 лет до общего предка. Столь большая погрешность вызвана малым числом гаплотипов в серии, причем гаплотипов коротких, и малым числом мутаций. Напомню, что расчет погрешности в данном случае проводится извлечением квадратного корня из трех (мутаций), что дает 1.732, далее его обратной величины (1/1.732 = 0.577), возведением ее в квадрат (0.577 = 0.333), прибавлением 0.01 (это – квадрат принятой погрешности величины константы скорости мутации, которая принимается равной ±10 %, то есть ±0.1), что дает 0.343, и, наконец, извлечением квадратного корня из последней величины, что дает 0.586 (то есть ±58.6 %). Это и есть величина погрешности определения времени до общего предка при трех мутациях в серии гаплотипов. При величине 1325 лет погрешность равна 1325x0.586, то есть ±780 лет.
Надо сказать, что в описанном (упрощенном) варианте есть много допущений. Допущения есть всегда, в любом варианте расчета погрешностей. Например, в данном случае мы принимаем, что погрешность определения константы скорости мутации в 12-маркерных гаплотипах (ее величина равна 0.02 мутаций на гаплотип на условное поколение) составляет ±10 %. Это – эмпирическая величина, полученная при изучении серии данных документальной генеалогии. Такую же погрешность мы принимаем и в случае 67-маркерных гаплотипов, хотя сопоставление ДНК-генеалогических данных с многочисленными данными документальной генеалогии показало, что реальная погрешность равна ±3 %, и в этом случае в примере выше к величине 0.333 следует прибавлять не 0.01, а 0.0009, и итоговая погрешность получится не ±58.6 %, а 57.8 %, что практически одно и то же. Это получается, потому что при всего трех мутациях именно столь малое их число практически полностью определяет погрешность времени до общего предка серии гаплотипов. Только при большом числе гаплотипов и большом числе мутаций общую погрешность начинает определять погрешность определения константы скорости мутаций. Например, при 1000 мутаций в серии гаплотипов погрешность вычисляется, как описано выше, извлечением квадратного корня из 1000 (мутаций), что дает 31.62, далее его обратной величины (0.0316), возведением ее в квадрат (0.001), прибавлением 0.01 (при 10 % погрешности величины константы скорости мутации), что дает 0.011, и, наконец, извлечением квадратного корня из последней величины, что дает 0.105 (то есть ±10.5 %). Это и есть величина погрешности определения времени до общего предка при 1000 мутациях в серии гаплотипов. При величине 1325 лет погрешность тогда равна 1325±140 лет. А если погрешность константы скорости мутаций равна ±3 %, то к величине 0.001 (после возведения в квадрат) следует прибавить не 0.01, а 0.0009, и итоговая погрешность получится не 10.5 %, а 4.4 %, или 1324±60 лет до общего предка.