Приведем пример. Имеем неоднородную выборку из 300 гаплотипов в 25-маркерном формате, в которой 200 гаплотипов происходят от общего предка, который жил 3000 лет назад, и 100 гаплотипов – от предка, который жил 800 лет назад. Если мы построим дерево гаплотипов, то сразу увидим, что 200 гаплотипов образуют одну большую и глубокую (высокую) ветвь, и 100 гаплотипов – плоскую ветвь. Тогда сразу можно разделить ветви, и каждую из двух ветвей обсчитывать отдельно. В первой ветви из 200 гаплотипов все 25-маркерные гаплотипы будут разными (то есть логарифмический метод с ними работать не будет), что уже покажет, что общий предок жил более 2500 лет назад (при 2500 годах в выборке могли бы быть два одинаковых гаплотипа, потому что [ln(200/2)]/0.046 = 100 условных поколений, или 2500 лет до общего предка). На все 200 гаплотипов будет 1104 мутаций от базового гаплотипа, что даст 1104/200/0.046 = 120 условных поколений, или 120х25 = 3000 лет до общего предка (вкладом возвратных мутаций здесь для простоты пренебрегаем).
Во второй ветви из 100 гаплотипов в 25-маркерном формате 23 гаплотипа будут идентичными друг другу. Это даст [ln(100/23)]/0.046 = 32 условных поколений, то есть 800 лет до общего предка. Иначе говоря, если смешать эти 200 и 100 гаплотипов, то в этой смеси 23 гаплотипа будут одинаковыми (из молодой ветви), и мы получим [ln(зоо/2э)]/о.046 = 56 условных поколений, то есть якобы 1400 лет до общего предка якобы одного для всех 300 гаплотипов. А мутаций во всей составной, неоднородной выборке будет 1251, если базовые гаплотипы обеих ветвей случайно совпадут. Тогда линейный метод даст 1251/300/0.046 = 91 условное поколение, или 2275 лет до якобы общего (фантомного) общего предка. Если базовые гаплотипы обеих ветвей будут разными, то время до фантомного общего предка будет практически любым между 3000 и 800 лет.
Итак, подводим итоги. Выборка составная, неоднородная, общие предки жили 3000 и 800 лет назад. Линейный метод дал фантомного общего предка 2275 лет назад, логарифмический -1400 лет назад. То, что эти времена не совпали друг с другом, говорит о том, что так считать нельзя, и выборки надо разделять. Обычно разделение проводится с использованием деревьев гаплотипов (см. следующий раздел).
Вопрос 40: Выборки в ДНК-генеалогии обычно несоизмеримо малые по сравнению с реальными величинами самих популяций. Как таким выборкам можно доверять? Есть "мнения", что выборки должны иметь как минимум 10 тысяч гаплотипов, чтобы получать относительно разумные данные.
Это совершенно ненаучная постановка вопроса, опять "по понятиям", по "мнениям", ни на чем не основанным. На это можно задать встречный вопрос, который уже был задан выше в настоящей книге – чтобы понять, что море соленое, нужно ли пробовать воду из всех бухточек? А как же химики делают анализ растворов, беря пробу всего лишь в долю миллилитра из ведра, цистерны, озера? Когда делают анализ крови, что, всю кровь из вас выкачивают? Нет. Значит, вопрос о размере пробы поставлен некорректно. Вопрос на самом деле сводится не к каким-то с потолка взятым числам, а к к тому, равномерно ли перемешана система, чтобы по малой пробе, или выборке, судить о всей системе. Этот вопрос в ДНК-генеалогии давно проработан, и результаты сопоставительных исследований показаны, например, в следующей таблице:
Таблица. История определений времени до общего предка гаплогруппы R1a на "пост-советском пространстве" по разным сериям гаплотипов.
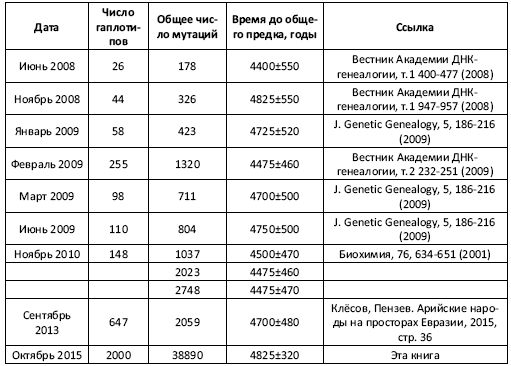
Из таблицы видно, что при последовательном переходе от серии из 26 гаплотипов до 2000 гаплотипов, и при увеличении числа мутаций в них в двести с лишним раз расчетное время до общего предка этих гаплотипов, в данном случае проживавшего на Русской равнине около пяти тысяч лет назад, получается практически одинаковым, в пределах погрешности расчетов. Это значит, что гаплотипы гаплогруппы R1a на пост-советском пространстве перемешаны достаточно хорошо, и все выборки вполне репрезентативны.
Конечно, могут быть и другие ситуации. Например, в горах в каждой долине состав гаплотипов (и гаплогрупп/субкладов) может заметно различаться, в отличие от того, что может наблюдаться на равнине, где гаплотипы более перемешаны за тысячелетия. Но в любом случае расчеты и выводы по гаплотипам относятся только к той конкретной выборке, которая рассматривалась, и только сопоставление разных выборок может показать, насколько система "перемешана", и решить вопрос об обобщении результатов расчетов и выводов на всю популяцию региона, или только ее конкретную часть. Но пока репрезентативность разных выборок наблюдается и в горах. Например, разные выборки осетин и карачаево-балкарцев дают воспроизводимые результаты для каждого из этих этносов. Перемешивание между ними обнаружено, но очень незначительное, практически не влияющее на результаты расчетов.
В большинстве случаев результаты расчетов почти не зависят от размера выборки (при числе гаплотипов больше двух-трех десятков), то есть они устойчивы к статистическим вариациям, если популяция достаточно перемешана и выборка произведена неупорядочено. Размер выборки увеличивает точность, и то только до определенных пределов. Это, повторяем, относится к довольно большим популяциям, которые перемешались за тысячелетия, но именно с такими обычно и работают.
Вопрос 41: Что такое "деревья гаплотипов" в ДНК-генеалогии?
По ходу изложения мы будем показывать деревья гаплотипов, которые отражают ДНК-картину этносов, родов, племен. Это вовсе не значит, что гаплотипы определяют этнос. Но они его в определенной степени описывают, каждый этнос по-разному. Человеку непривычному эти деревья представляются некими абстрактными образованиями, но в них на самом деле заключен большой смысл и в их графическом виде дается большой объем информации. Для того чтобы сделать деревья в этой книге более понятными и осмысленными, приведем несколько вводных, "модельных" примеров.
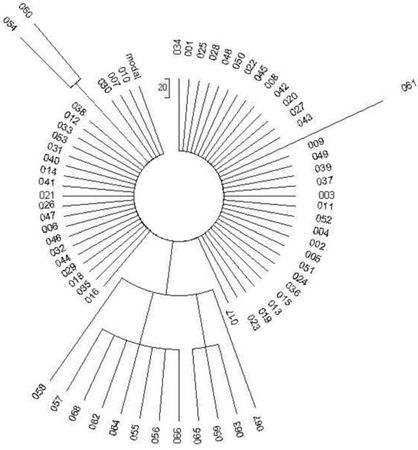
Рис. 7. Дерево, состоящее из 68 гаплотипов гаплогруппы R1a в их 6-маркерном формате. Базовый гаплотип здесь 13 25 15 11 12 11 (в системе DYS 393, 390, 19, 391, 388, 392). Базовые гаплотипы образуют "гребенку" на дереве.
На рисунке выше приведено дерево реальной выборки из 68 гаплотипов гаплогруппы R1a. Гаплотипы простенькие, 6-маркерные, общий предок всех жил всего 625 лет назад, так что мутаций в гаплотипах набежало мало. Можно даже заранее посчитать, сколько. Это дерево гаплотипов потомков Джона, Лорда Британских островов, который жил в 14-м веке и умер в 1386 году. Его потомки – известный шотландский клан Мак-Доналдов (один из Мак-Доналдов был маршалом у Наполеона). Константа скорости мутации для 6-маркерных гаплотипов равна 0.0074 мутаций на гаплотип на условное поколение в 25 лет. Тогда за 625 лет (25 условных поколений) в каждом гаплотипе набежит 0.0074х25 = 0.185 мутаций, и на все 68 гаплотипов будет 0.185х68 = 13±4 мутаций. Погрешность рассчитывается по обычным правилам математической статистики.
Смотрим на дерево гаплотипов. Там – 15 мутаций, то есть в пределах погрешности. Можно посчитать самим, это все "вылезающие" из колеса спицы. А вылезают они в разных (и заранее непредсказуемых) местах, потому что мутации происходят неупорядоченно. 53 гаплотипа не мутированы, они образуют ровную гребенку, или "колесо" вокруг центральной части. Это – тот же самый гаплотип, что имел общий предок всех 68 человек, то есть Джон, Лорд Островов:
13 25 15 11 12 11
53 человека этот гаплотип полностью сохранили, потому что 625 лет – это относительно малое время, и 15 мутаций – это все отклонения от предкового гаплотипа, что за это время смогли произойти.
Показанные выше шесть чисел соответствуют шести участкам в Y-хромосоме ДНК, в которых повторяются выбранные исследователями короткие нуклеотидные последовательности. В первом участке – 13 повторов, во втором – 25 повторов, в третьем – 15 повторов и т. д. Мутация – это изменение числа повторов. Ошибся копирующий фермент при биологическом копировании Y-хромосомы, скопировал третий участок не 15 раз, как завещали предки, а 16 раз, получилось
13 25 16 11 12 11
Это – два идентичных гаплотипа, на дереве выше под номерами 054 и 060. С правой стороны – гаплотип 061, он имеет вид
14 25 15 11 12 11
У него мутация проскочила в первом участке, было 13 повторов, стало 14. То есть опять система копирования ошиблась в сторону завышения числа повторов. А вот в семерке идентичных гаплотипов под номерами 055–057, 062, 064, 066, 068 – мутация прошла во втором участке, на понижение (25 → 24) и получилось
13 24 15 11 12 11
Действительно, этот участок, или маркер, как их называют, один из самых подверженных мутациям. Теория подсказывает, что в первом участке на все гаплотипы произойдет только одна мутация, во втором – семь мутаций, в третьем – две мутации. Так и получилось на практике. То есть даже при такой малой статистике закономерности в целом выполняются. Более того, все остальные пять мутаций на дереве гаплотипов относятся к тому же (второму) быстрому маркеру. Гаплотипы под номерами 059, 063 и 065 имеют вид